Koska maailma tuntuu siirtyneen faktojen jälkeiseen aikaan, myös täällä Pulmakulmassa lienee tarpeen venyttää totuuden rajoja. Osoitetaan matemaattista induktiota käyttäen, että kaikki suomalaiset ovat samanikäisiä.
Matemaattisessa induktioperiaatteessahan on kyse siitä, että jos voidaan osoittaa, että
- jokin luonnollisia lukuja tai jotain sen osajoukkoa koskeva väittämä pätee pienimmälle tarkasteltavalle luvulle, ja että
- väitteen totuudesta luvulle
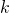 seuraa väitteen totuus luvulle
seuraa väitteen totuus luvulle 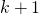 ,
,
niin tällöin väite pätee kaikille tarkasteltaville luvuille. Induktioperiaatteen hyvä havainnollistus löytyy esimerkiksi tästä.
No niin, sitten asiaan. Osoitetaan ensin, että yhden ihmisen joukossa kaikki ovat keskenään samanikäisiä. Tämä on tietenkin triviaalisti totta.
Tehdään seuraavaksi induktio-oletus, että 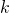 suomalaisen joukossa kaikki ovat samanikäisiä. Riittää osoittaa, että tästä seuraa se, että sattumanvaraisten
suomalaisen joukossa kaikki ovat samanikäisiä. Riittää osoittaa, että tästä seuraa se, että sattumanvaraisten 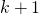 suomalaisen joukossa kaikki ovat samanikäisiä. Tämä voidaan todistaa osoittamalla, että tämän joukon sattumanvaraiset henkilöt
suomalaisen joukossa kaikki ovat samanikäisiä. Tämä voidaan todistaa osoittamalla, että tämän joukon sattumanvaraiset henkilöt 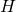 ja
ja 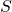 ovat samanikäisiä.
ovat samanikäisiä.
Poistetaan ensin 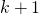 suomalaisen joukosta henkilö
suomalaisen joukosta henkilö 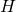 . Nyt jäljelle jääneet kaikki
. Nyt jäljelle jääneet kaikki 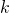 suomalaista ovat induktio-oletuksen mukaan samanikäisiä. Siis
suomalaista ovat induktio-oletuksen mukaan samanikäisiä. Siis 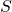 on samanikäinen kaikkien muiden kanssa, esimerkiksi henkilön
on samanikäinen kaikkien muiden kanssa, esimerkiksi henkilön 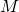 kanssa. Poistetaan seuraavaksi alkuperäisestä
kanssa. Poistetaan seuraavaksi alkuperäisestä 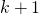 suomalaisen joukosta henkilö
suomalaisen joukosta henkilö 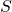 . Nyt jäljelle jääneet
. Nyt jäljelle jääneet 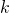 henkilöä ovat induktio-oletuksen mukaan samanikäisiä. Siis esimerkiksi
henkilöä ovat induktio-oletuksen mukaan samanikäisiä. Siis esimerkiksi 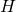 ja
ja 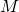 ovat nyt samanikäisiä.
ovat nyt samanikäisiä.
Mutta nythän toisaalta 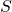 ja
ja 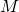 ovat samanikäisiä ja toisaalta
ovat samanikäisiä ja toisaalta 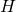 ja
ja 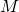 ovat samanikäisiä, joten välttämättä
ovat samanikäisiä, joten välttämättä 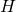 ja
ja 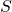 ovat samanikäisiä. Olemme siis onnistuneet osoittamaan, että
ovat samanikäisiä. Olemme siis onnistuneet osoittamaan, että 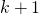 suomalaisen joukossa kaikki ovat samanikäisiä. Induktioperiaatteen mukaan kaikki suomalaiset ovat samanikäisiä!
suomalaisen joukossa kaikki ovat samanikäisiä. Induktioperiaatteen mukaan kaikki suomalaiset ovat samanikäisiä!
No, tuota. Oikeasti minä en ole samanikäinen veljeni kanssa. Viikon vaikea pulma on selvittää, mikä meni pieleen. Onko matematiikka rikki?
Ratkaisu: Matematiikka ei onneksi ole rikki, vaan todistuksessa on ihan oikea virhe. Henkilöistä 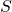 ja
ja 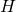 poikkeavan henkilön
poikkeavan henkilön 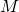 olemassaoloa ei voida olettaa. Jotta näin voitaisiin tehdä, olisi pitänyt pystyä osoittamaan, että kaikissa kahden henkilön joukoissa on vain samanikäisiä. Ja tämähän ei tietenkään onnistu.
olemassaoloa ei voida olettaa. Jotta näin voitaisiin tehdä, olisi pitänyt pystyä osoittamaan, että kaikissa kahden henkilön joukoissa on vain samanikäisiä. Ja tämähän ei tietenkään onnistu.

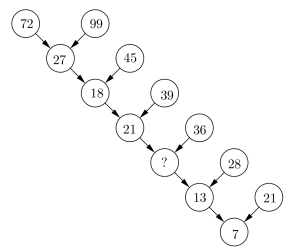 Tämä erityisen kaunis pulma on peräisin Nob Yoshigaharalta (1930–2004), japanilaiselta ongelmaspesialistilta. Minä löysin sen jälleen kerran Alex Bellosin kautta.
Tämä erityisen kaunis pulma on peräisin Nob Yoshigaharalta (1930–2004), japanilaiselta ongelmaspesialistilta. Minä löysin sen jälleen kerran Alex Bellosin kautta.




